はじめに
近年のSSL用ロボットはフィールドの大型化に対応するためにモーターの高出力化が進んでいるようだ。私が現役だった2014年まではEC 45 flat 30Wモーターを用いていたが今は70Wのモーターに換装されていた。その70Wモーターに電力を供給するためバッテリーも高電圧化し現在のロボットは6セルのLiPoバッテリーから給電されている。しかもモーターは48V品なのでバッテリーの約24Vから2倍圧昇圧回路を通じて約48Vを生成している。48V品をわざわざ採用した理由は24V品に流れる電流がDRV8332(モータードライバIC)の定格電流に収まらなかったからだそうだ。
今回、回路基板を新規設計するにあたってはこの昇圧回路をメイン基板に内蔵することを目標とした。
評価基板の作成
4つの車輪用モーター(とドリブル用モーター)を70Wで駆動するために48V電源の出力は10Aあったら十分だろうということで目標は48V/10A出力の電源の設計である。一発で作るのは怖いのでまず評価基板を作って動作確認をすることにした。
以下が製作した評価基板のブロック図と写真である。
 |
| 評価基板のブロック図 |
 |
| 評価基板の写真 |
この基板は左側のピンソケットを他の評価基板と接続して使用することを前提としている。他の評価基板に主要な電源を供給するために48V昇圧回路以外に5.1Vと12Vのレギュレータも搭載することにした。
この評価基板は外付けのスイッチで電源をオンオフするようにできているが、スイッチがオフのときでもVBATと5.1Vは他の評価基板に供給できるようにできている。なぜかというとスイッチがオフされたことを検知して回路の電源を安全にシャットダウンできるようにするためである。メイン基板にJetson NanoやRaspberry Piを搭載する場合、スイッチが切られたときにシャットダウン処理を行う時間が確保できないとファイルシステムを破損するおそれがある。かといってスイッチを切る前にシャットダウンボタンを押すという操作をするのは煩雑である。そこでスイッチをオフしたらモーターが停止し、遅れてJetsonがシャットダウンできるようにした。
回路設計
12Vおよび5.1VレギュレータについてはそれぞれのICのデータシートを参照してもらうとしてここでは48Vレギュレータの回路設計について解説する。48Vレギュレータには10Aという高電流出力が要求されること、リップル電流を抑えてパスコンを減らしたいこと、発熱源を分散させたいことから2相インターリーブ化することにした。制御ICはLTC3862-1を選定した。このレギュレータは6セルのLiPoバッテリーから給電されるのである程度の入力電圧の変動を見込んでおかなくてはいけない。入力電圧範囲は20~26Vとした。
動作原理
レギュレータの簡易的な回路図を以下に示す。この方式の回路は昇圧チョッパと呼ばれる。
昇圧チョッパの動作原理を説明する。初期状態でインダクタ電流IL=0、COUTはVOUT=VINまで充電されているものとする。この状態でMOSFETをオンするとVSW≒0となり、下図の赤線で示す経路でインダクタとMOSFETに電流が流れ始める (ID=IL)。ダイオードは逆バイアス状態となりオフになる (IF=0)。ILはインダクタの性質により一定の割合でゆっくりと増加していく。
一定時間経つかILが閾値を超えるとMOSFETがオフする。電流を維持しようとするインダクタの働きによりVSWが上昇し、VSW=VOUT+VFに達するとダイオードに電流が流れ始める (IF=IL)。VFはダイオードの順方向降下電圧である。ILは徐々に減少していく。この電流によりCOUTが充電されVOUT電圧が増加する。
MOSFETがオン・オフを繰り返しCOUTがさらに充電されていく。
もちろんこのままでは際限なくVOUTが増加していってしまうので制御ICにより一定電圧を維持するようにオン時間が制御される。定常状態においてILは以下のような波形になる。なおこの図はfSWが固定かつ連続導通モード(CCM)を想定している。軽負荷時や不連続導通モード(DCM)、臨界導通モード(CRM,BCM)のレギュレータでは異なった波形となる。
固定周波数のCCMレギュレータの定常状態におけるデューティ比Dは入出力電圧にのみ依存する。
$$D={V_{OUT}+V_F-V_{IN} \over V_{OUT}+V_F}$$
入力電流IIN、出力電流IOUTには以下の関係がある。
$$I_{IN}={I_{OUT} \over 1-D}$$
リップル電流ΔILは以下の式で与えられる。ΔILは最大負荷時のIINの30%程度が目安とされている。ΔILはLとfSWで調整できる。
$$\Delta I_L={V_{IN} D \over L f_{SW}}$$
LとfSWが最適点から外れていると例えば以下のような問題が起きる。
Lが小さすぎる → ILpkが大きくなり抵抗損失が増える。
Lが大きすぎる → インダクタのサイズが大きくなる。
fSWが小さすぎる → ILpkが大きくなり抵抗損失が増える。パスコンが多く要る。
fSWが大きすぎる → MOSFETのスイッチング損失とCoss損失が増える。
あちらを立てればこちらが立たずといった感じで電源設計はバランスを取りながら行うものである。
インダクタの選定
インダクタのデータシートには以下の表の値が記載されている。インダクタの選定で重要なのが飽和電流Isatである。Isatを超える電流を流すとコアの飽和によりインダクタンスが減少する。スイッチングレギュレータにおいてはインダクタが飽和すると1回のスイッチングサイクルでインダクタに蓄えられるエネルギーが減少してしまうため最大出力電流が設計より少なくなる問題が発生する。
| パラメータ | 意味 |
|---|---|
| インダクタンス L | あるテスト周波数でのインダクタンスである。 |
| 直流抵抗 DCR | 直流電流に対する抵抗値である。 |
| 定格電流 Irms | インダクタに直流電流を流すと直流抵抗により発熱を生じる。 一定の温度上昇ΔTが生じる直流電流値を定格電流Irmsとする。 ΔTは40℃とされていることが多い。 実際の発熱は基板レイアウトによって異なるので目安である。 |
| 飽和電流 Isat | インダクタに大きな電流を流すとコアが飽和して一時的にインダクタンスが減少する。 インダクタンスが定格からΔL減少したときの電流値を飽和電流Isatとする。 ΔLは定格インダクタンスの30%とされていることが多い。 |
| 自己共振周波数 SRF | インダクタのインダクタンスと巻線間の寄生容量による共振の周波数である。 SRFより低いスイッチング周波数でインダクタを使用しなければいけない。 寄生容量を見積もれなくもない。 |
| 共振のQ | あるテスト周波数でのインダクタのリアクタンス÷AC抵抗の値である。 AC抵抗がどの程度なのかの見積もりに使えなくもない。 |
インダクタの選定にあたって最大負荷時のILpk,maxが飽和電流Isatを超えていないこと、IINがインダクタの定格電流Irmsを超えていないことを目安にすることになる。最大負荷時とは今回のケースではVIN=20VでIOUT=5A (1相あたり)のときである。L=10uH、VF=0.6V、fSW=330kHzとして具体的な値を計算すると
\begin{eqnarray} D_{max}=\mathrm{48[V]+0.6[V]-20[V] \over 48[V]+0.6[V]}=0.5885 \\ I_{IN,max}=\mathrm{5[A] \over 1-0.5885}=12.15 \mathrm{[A]} \\ \Delta I_{L,max}=\mathrm{20[V] \times 0.5885 \over 10[uH] \times 330[kHz]}=3.567 \mathrm{[A]} \\ I_{Lpk,max}=I_{IN,max}+\Delta I_{L,max}/2=13.94 \mathrm{[A]} \end{eqnarray}
今回はSRP1265A-100Mを選んだ。このインダクタはIsat=15.5Aなので飽和は起こさないがIrms=10.0Aなので発熱が過剰となるおそれがある。しかし実際のロボットにおいて高負荷が連続することは少ないだろうし高負荷が連続しないようにモーターの電流を制限すれば良い話である。
MOSFETの選定
まずMOSFETのドレインソース間電圧VDSの耐圧と連続ドレイン電流IDについて考える。
MOSFETのVDSにはVOUT+VFに等しい48.6Vが加わる。しかし現実には回路の寄生インダクタンスに起因するリンギングによってそれ以上の電圧がVDSに加わることになる。フライバックと比べれば昇圧チョッパのリンギングは大きくないので30%のマージンをとり80V程度のVDS耐圧を持つMOSFETを選定する。
次にIDは最大負荷時に平均7.15Aが流れる。これに対してマージンを加えた定格電流を持つMOSFETを選定すればいい。ただIDに関しては放熱的に定格ギリギリまで流すことは難しいものであるし、オン抵抗RDSが妥当なMOSFETを選べば勝手に条件を満たすものなので深く考える必要はないかもしれない。
必要なVDS, ID定格が分かったらコストが高すぎず損失ができるだけ小さくなるように選定を行う。損失の計算方法はMOSFETの損失の計算を参照されたい。
MOSFETを選ぶ際はむやみにRDSの小さいものを選べばよいというものではない。RDSの小さいものは寄生容量が大きくCoss損失とスイッチング損失が大きくなるためかえって総合的な損失が増えることがあるからである。またVDS耐圧が同じもの同士を比べるとRDSが小さいほどチップ自体が大きくなるのでコスト面からも勧められない。
MOSFETは非常に品種が多いがその中から目的の用途にあったものを簡単に見つける方法がある。それはデータシートのテスト条件を見ることである。特に遷移時間に関する項目のテスト条件はメーカーの想定するその素子の使い方に近いと思われる。少なくともあまりに不適当な条件が書かれていることはないだろう。
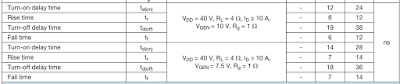 |
| 例1 SiSS30DNのスイッチングテスト条件(VDS=40V, ID=10A) |
 |
| 例2 GS66508Tのスイッチングテスト条件(VDS=400V, ID=16A) |
目的に近いテスト条件の書かれたMOSFETを見つけたらそのRDS, Ciss, Cossが目的の用途として妥当なMOSFETのパラメータである。その値付近で好みのMOSFETを探そう。
今回はSiSS30DNというVDS耐圧80V、RDS,max=8.25mΩのMOSFETを選定した。
ダイオードの選定
整流ダイオードにはMOSFETと同じだけの逆バイアス電圧が加わるので同等の耐圧VRRMが必要である。今回は必要な耐圧が80Vと低いのでショットキーバリアダイオード(SBD)が使用できる。もし高い耐圧が必要ならSBDと比べて損失の大きいスイッチングダイオードやファストリカバリダイオード(FRD)から選ぶことになる。
ダイオードに流れる最大の平均電流はIOUTの最大値に等しい。ダイオードの定格平均電流IF(AVG)はそれにマージンを加えた値以上であれば良い。
今回のIOUTの最大値は5Aであるのでそれに30%のマージンを加え、IF(AVG)が8A以上のSBDを探すことにした。今回はかなり余裕を持たせてVRRM=100V, IF(AVG)=15AのV15PM10を採用したが、VRRM=100V, IF(AVG)=10AのV10P10を選択したほうが接合容量Cjが小さくなるためMOSFETのCoss損失が減り効率向上が望めただろう。
損失計算
インダクタの損失
インダクタの損失は直流抵抗成分によるDC損失とAC抵抗成分とコアロスによるAC損失の和で計算できる。直流抵抗成分はインダクタの巻線抵抗から生じる。この値はインダクタのデータシートにDCRとして記載されている。AC抵抗成分は巻線の表皮効果と近接効果で巻線抵抗が高周波で増加することで生じる。通常、AC抵抗とコアロスがどの程度かはインダクタのデータシートに記されておらず、測定条件によっても変わる値なので知りたいなら実測するしかない。
DC損失は以下の式で計算できる。SRP1265A-100MのDCRは最大値の16.5mΩを用いた。
\begin{eqnarray} \mathrm{DC損失} P_{L,DC} &=& \mathrm{DCR} \times I_{IN}^2 \\ &=& \mathrm{16.5[mΩ] \times 12.15[A]^2} = 2.44 \mathrm{[W]} \end{eqnarray}
AC損失の正確な値はデータが無いため計算できない。しかしQの値から100kHzにおけるAC抵抗成分が最大でも0.314Ωであるとわかる。表皮効果によるAC抵抗は周波数の平方根に比例するので330kHzでは\(\sqrt{3.3}\)倍して0.571Ωであるとする。これだけを用いて仮にAC損失を計算すると以下のようになる。ここでΔILを\(\2\sqrt(3)\)で割っているのは三角波の実効値を求めるためである。
\begin{eqnarray} \mathrm{AC損失} P_{L,AC} &=& \mathrm{ACR} \times ({\Delta I_L \over 2 \sqrt{3}})^2 \\ &=& \mathrm{0.571[Ω] \times ({3.567[A] \over 2 \sqrt{3}})^2} = 0.605 \mathrm{[W]} \end{eqnarray}
MOSFETの損失
詳細はMOSFETの損失の計算を参照されたい。SiSS30DNについて損失を計算すると以下のようになる。
\begin{eqnarray} \mathrm{導通損失} P_{main,cond} &=& 0.722 \mathrm{[W]} \\ \mathrm{C_{oss}損失} P_{main,coss} &=& 0.159 \mathrm{[W]} \\ \mathrm{スイッチング損失} P_{main,sw} &=& 0.707 \mathrm{[W]} \end{eqnarray}
ダイオードの損失
ダイオードの損失はダイオードに電流が流れているときにVFの分だけ電圧がドロップするこによる損失である。簡単のため電流に関わらずVF=0.6Vとする。
\begin{eqnarray} \mathrm{ダイオード損失} P_{diode} &=& V_F I_{IN,max} (1-D) \\ &=& 0.6 \times 12.15 \mathrm{[A]} (1-0.5885) = 3.00 \mathrm{[W]} \end{eqnarray}
熱設計
以下に評価基板の簡略化した熱回路網を示す。ダイオード・MOSFET・インダクタ等の素子から基板への熱抵抗θjd1b, θjt1b, θjd2b, θjt2bと基板から周囲への熱抵抗θbaだけでモデル化した。インダクタとMOSFETは同じ個所から発熱すると仮定した。基板レイアウトは対称なので計算上はθjd1b=θjd2b, θjt1b=θjt2bであるとして扱う。(本当は配置場所の違いによりわずかに差異がある)
 |
| 簡略化した熱回路モデルと基板レイアウト(L1面) |
これらの熱抵抗が実際の基板でどの程度の値になっているか測定した。
まずダイオードの熱抵抗θjd1b, θjd2bだが、ダイオードの順方向に一定電流を流して回路各部の温度を測定した。2相のダイオードは回路的に分離できないので電流は2相のダイオードに等しく流れるものとして扱った。測定結果よりθjd1b, θjd2b=14.6℃/Wと分かった。
| Vf[V] | If[A] | Ta[℃] | Tb[℃] | Tjd1[℃] | Tjd2[℃] | θjd1b[℃/W] | θjd2b[℃/W] | θba[℃/W] |
| 0.343 | 0.5 | 24.3 | 26.9 | 29.2 | 29.2 | 13.4 | 13.4 | 7.58 |
| 0.375 | 1 | 24.9 | 28.4 | 34.3 | 34.6 | 15.7 | 16.5 | 4.67 |
| 0.378 | 1.5 | 25.6 | 32.7 | 40.6 | 41.4 | 13.9 | 15.3 | 6.26 |
| 0.391 | 2 | 26.3 | 35.2 | 45.7 | 46.8 | 13.4 | 14.8 | 5.69 |
| 平均 | 14.6 | 6.05 | ||||||
続いてMOSFETの熱抵抗を測定した。MOSFETのゲートをドレインに直結した状態でVDSを印加してIDが流れるようにして温度を測定した。この測定はMOSFET1に対してのみ行った。測定結果よりθjt1b, θjt2b=12.6℃/Wと分かった。
| Vds[V] | Id[A] | Ta[℃] | Tb[℃] | Tjt1[℃] | θjt1b | θba |
| 2.22 | 0.1 | 25.6 | 26.1 | 28.5 | 10.8 | 2.25 |
| 2.19 | 0.2 | 25.5 | 27.7 | 32.8 | 11.6 | 5.02 |
| 2.19 | 0.3 | 26.8 | 28.8 | 37.7 | 13.5 | 3.04 |
| 2.20 | 0.4 | 26.8 | 30.0 | 41.8 | 13.4 | 3.64 |
| 2.20 | 0.5 | 26.9 | 31.2 | 46.0 | 13.5 | 3.91 |
| 平均 | 12.6 | 3.57 | ||||
2つの測定結果から分かるように測定対象によってθbaが違うのですでにモデルが破綻しているような気もするが間をとってθba=5℃/Wとすることにする。
各素子の損失の設計値はVIN=20V, IOUT=10A(1相あたり5A)のとき
\begin{eqnarray} \mathrm{MOSFET1,2の損失} P_t &=& 1.59 \mathrm{[W]} \\ \mathrm{ダイオード1,2の損失} P_d &=& 3.00 \mathrm{[W]} \\ \mathrm{インダクタ1,2の損失} P_i &=& 3.04 \mathrm{[W]} \end{eqnarray}
よって周囲温度からの基板温度と各素子の温度上昇は
\begin{eqnarray} \mathrm{基板温度上昇} \Delta T_b &=& \theta_{ba} \times 2 \times (P_t+P_d+P_i) = 76.3 \mathrm{[℃]} \\ \mathrm{ダイオード温度上昇} \Delta T_{jd1} &=& \Delta T_b+\theta_{jd1b} \times P_d = 120 \mathrm{[℃]} \\ \mathrm{MOSFET温度上昇} \Delta T_{jt1} &=& \Delta T_b+\theta_{jt1b} \times (P_t+P_i) = 135 \mathrm{[℃]} \end{eqnarray}
どうやら自然空冷ではこの評価基板を放熱しきれないようだ。もしIOUTを8Aまで絞れば損失は
\begin{eqnarray} \mathrm{MOSFET1,2の損失} P_t &=& 1.19 \mathrm{[W]} \\ \mathrm{ダイオード1,2の損失} P_d &=& 2.40 \mathrm{[W]} \\ \mathrm{インダクタ1,2の損失} P_i &=& 2.16 \mathrm{[W]} \end{eqnarray}
にまで減少し、温度上昇は
\begin{eqnarray} \mathrm{基板温度上昇} \Delta T_b &=& 57.5 \mathrm{[℃]} \\ \mathrm{ダイオード温度上昇} \Delta T_{jd1} &=& 92.6 \mathrm{[℃]} \\ \mathrm{MOSFET温度上昇} \Delta T_{jt1} &=& 99.7 \mathrm{[℃]} \end{eqnarray}
まで抑えられる。これならば自然空冷でも室温でなら各素子のTj,maxを下回ることができる。
実験
TODO 効率データがここに載る。
最終形
最終的な基板では出力電流を8Aに絞ったバージョンを採用した。以下に回路図を抜粋する。フィードバック抵抗は耐圧を確保するためR24,R29の2つに分割している。
 |
| Phoenix基板の48Vレギュレータの回路図 |
以下にレイアウトを示す。評価基板より基板がかなり大きくしかも6層基板なので熱的な余裕はあるはずである。
 |
| Phoenix基板の48Vレギュレータ(赤線で囲った部分) |

0 件のコメント :
コメントを投稿